The UK’s Office of National Statistics released the latest (and, I believe, the last) iteration of mortality rates in England by COVID vaccination status on 25 August 2023.
This new version, updated to link with Census 2021 data, stretches from April 2021 (when Census21 data starts being available) to May 2023. There’s a huge amount in it, but this headline chart from Table 1 communicates it well; the all-cause age-adjusted rates look like this.
The naïve may think this is simple and clear.
Age-adjusted all-cause death rates are not a complex concept, though they need solid age-linked data to put together. The “age-adjustment” bit tells you they’ve reweighted the age-distributions of groups to a single age profile, so different populations can be compared like-for-like. “All-cause deaths” are what they sound like: all deaths, from any cause at all. And the take-away appears clear: that vaccinated people have lower all-cause death rates than the vaccinated - and the shape of the signal is striking, while also being unsurprising.1
And the naïve are - in this case - quite right.
However, imagine you are - for whatever reason - strongly motivated to deny this conclusion, and instead want to manipulate the data until it appears to demonstrate the opposite.2
This might seem a challenge, but in fact it’s not that difficult - so long as your audience is low-information, and does not have too much statistical sophistication. It’s just intensely unethical.
Let’s work our way upwards through four levels of deceit - each level roughly corresponding to an increasing amount of work it takes to paint your new story.
Level 1 - Just lie:
It’s easy to dismiss this approach, but I think it’s a mistake to look down on well-worn strategies, just because they’re simple.
Here’s a good one.
They only count people as vaccinated from two weeks after the dose! That’s what you’re looking at when you see high death rates in the “unvaccinated” - it’s people dying from the jab!
This lie is very attractive. It explains why the unvaccinated group have higher death rates, AND it shifts the blame onto the vaccines, all in one go. What's more, it’s plausible, in the sense that some (different) efficacy studies did leave a window to allow the vaccine to become effective Now you can attribute all the difference between the groups to the deadly effects of the vaccines
One issue is that the death rates don’t do what they should do if this lie were true. They should run down the ages of the “unvaccinated” as the vaccine roll-out ran down the ages. They don’t. The wrong people die, with the elevated deaths stubbornly remaining highest in the older unvaccinated groups - rather as you’d expect if it were COVID that was the driver of the death rates.
A second, more fundamental issue is that not only is the above a lie, it’s an obvious lie, and any neutral party will be able to discover this with a five-second search.
In their study, the ONS count individuals as vaccinated from the moment of vaccination. They make it very clear, over and over, in every article and every set of notes on the data. The short methodology briefing on the page you download their data from, states it right up front.
Given these kind of statements, I do feel for whichever analyst in the ONS has been handed a sheaf of freedom-of-information requests and has to type out this reply to the mildly unhinged over and over and over, while remaining scrupulously polite:
Q:
A:
As a result, while a simple lie is still - deservedly - a popular move, you’re running a risk. Someone might notice and call you out. What if you’re targeting a more sophisticated audience: one that can read. What then?
Level 2 - Rail against age standardisation:
The UK - like many countries - had a prioritised approach to vaccine roll out: old and vulnerable first. As a result, the age profile of vaccinated and unvaccinated people tends to be very different. In early 2021 only 75+s had been called forward for vaccination, plus a few NHS personnel. So, the average age of the vaccinated cohort at the start of the dataset was around 80, while the average age of unvaccinated was around 35.
Comparing the raw death rates of these two groups will indeed make the vaccine look dangerous. It would also make a nice cup of tea and a sit down look dangerous. So the rates in the chart above are age-standardised to solve this issue - as are all principled approaches of this kind.
However, it must be admitted, age-standardisation can look scary. The ONS give the formula like this:
So the obvious line to take is that since this looks absurd and complicated, it must be invalid. It must be manipulation of the figures. Just give the raw numbers. What are you afraid of? (Sprinkle various appeals to “common sense” and “stop the manipulation” in there.)
There are two issues with this move. The first is that anyone mathematically literate will look at the equation above and tell you there’s nothing underhand going on, it’s just a weighted average by age. That is, all the ASMR is doing is taking the death rates for each age group, and then taking an average weighted by the populations in the “ESP” - the “European Standard Population”. And since everyone is being reweighted to the same profile, this is indeed a reasonable procedure to give you a comparable death rate - it will give you the overall death rate for a population with an age-profile like the ESP (which, for most European countries, will be pretty similar to the actual age profile of the population).
Assuming you are able to ignore and shout down these people as spouting technobabble, there is a second issue. If someone does just remove the effects of the age-standardisation by comparing age-group by age-group, then it becomes clear very quickly that the age-standardisation is not distorting things - it’s bringing out the true pattern.
But, again, there won’t be many of these people: you can shout them down. Use rhetoric like demanding that you look at all the data (i.e., the total of all ages) and it’s not “manipulated” at all. If you do this, then at least in early 2021, you can happily compare the death rates in the vaccinated group (average age ~80) vs death rates in the unvaccinated group (average age ~35).3 And you should be able to make a lot of mileage out of this, for every person who spots what you’re doing.
Level 3 - Switch denominators:
The all-cause mortality rate is a rate “per 100k person-years”. There was an old trick of ignoring this rate as “more manipulation” and pointing out on a raw count, more vaccinated people than unvaccinated people were dying. But almost no-one is so stupid to go for that now. With vaccination rates of 80%+ across the population, almost everyone can spot that there are a lot more vaccinated people than unvaccinated. So, you need to be more sophisticated.
Here’s a smarter approach. The ONS built their rates “per 100k person-years” by matching everyone’s vaccination records that they could to the Census 2021 data. This gave them a population of people where they had all the data they needed (vaccination status, age, sex), which gives them around 91.6% of the population measured on Census day 2021. So their death numbers are for that population, and their rates per 100k are for that population of NHS-record-linked people.
But what if you changed that?
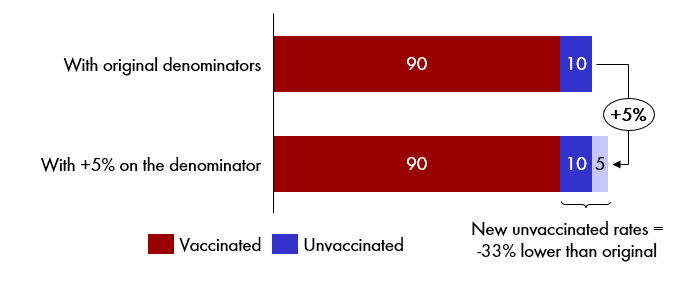
It’s a surprising mathematical fact that with the high vaccination rates we saw in England - 90%+ in many age-groups - a very, very small change in your denominator (the population you are measuring rates over) can drive a very large change in the rate for the unvaccinated cohort. This is because the unvaccinated group are difficult to count directly, so you obtain the number by taking the total denominator, and then subtracting the (known) vaccinated number. Higher denominator = larger apparent unvaccinated population to spread death numbers over = lower rates.
I think the simplest way of showing the surprising size of this effect is with a notional diagram - here, a relatively small +5% inflation of the denominator leads to a -33% suppression of all rates (death rates, hospitalisation rates, infection rates) in the unvaccinated.
Now, given we are talking about all-cause mortality rates, a -33% suppression in a death rate is easily enough to shrink, or even reverse all the positive effects of the vaccine, and make it look as though it is elevating death rates. All you need to do is find a way of substituting in a denominator that’s 5% larger.
Fortunately, this is very easy. The National Immunisation Management System maintains a list of everyone qualified for vaccination. And - due to a combination of duplication (people register at more than one GP surgery), and failure to remove those who emigrate, these NIMS lists are significantly larger than any other estimates of UK population.
Here are NIMS denominators for England vs the numbers Census 2021 found.
As is obvious, for many age-groups, the differences are much, much larger than the +5% we gave in the example above. So if you substitute in these NIMS denominators, “unvaccinated” death rates will be suppressed by enormous amounts (usually they’ll be halved, or even more). And given that we are looking at all-cause death rates, and COVID deaths are only a small fraction of those … this manipulation is guaranteed to make any vaccine: even a 100% effective, 100% safe one, appear hugely dangerous.
Given you get such a powerful effect for what looks rather like a small, unimportant change, this manoeuvre is extremely popular. The only price is a small note in the method or a footnote to explain why the numbers look different to the ONS’ ones (“we have used denominators from the UK’s national immunisation management service”), and you can even give them the wrong name to muddy the waters (“UKHSA denominators” - because the UKHSA used them briefly, before having a blistering letter from the UK’s statistical regulator pointing out exactly the issues shown here).
The vulnerability of this technique is that anyone who goes to the trouble of understanding what the ONS has done, will also realise there is only one motivation for an analyst to switch out the denominators. The ONS rejected the entire approach of counting deaths in the overall population for precisely the reasons outlined above: they concluded that - even with a Census, it was simply impossible to get the population estimates precise enough that the “unvaccinated” rates would be in any way reliable (they’d need to be correct to within <0.1% to give a useful rate comparison). And the ONS - better than most - would have known perfectly well that this was impossible.
So, the ONS took a smaller population (91.6% of Census 2021 numbers) for which they can count directly both the numbers of vaccinated and unvaccinated people, by counting their NHS records. The analysis they published is counting deaths amongst this smaller population, and giving the rates for this smaller population: a price of missing 8.6% to in exchange for accurate denominators, and therefore accurate rates.
Switching to a different denominator, and in particular, the much larger NIMS denominator, unpicks this entire careful project, and makes the results nonsense. So, if you do this, your motivation is transparent.4 But this takes time to explain and to understand. Almost no-one will go to the trouble, and they’ll be geeks, who - again - you can shout down, insult and ignore.
Switching the denominators is almost unbeatable.
Almost.
Level 4 - Mine down to tiny, atypical subgroups:
Returning to that chart of death rates by age, let’s now focus in on the youngest group shown:
Right at the start of the roll-out for 18-39 year olds, we have what a moment of promise. The death rates for this youngest cohort are more than twice as high in the vaccinated than the unvaccinated (for two months, and then the pattern reverses, but still).
What’s going on here, and can we use this to mislead?
Absolutely we can.
What’s going on is down to that prioritised roll-out again. In March to April of 2021 almost no 18-35 year olds qualified for a dose of the vaccine. It was only opened to <35s in late May. The only ones who got a dose before then (outside the relatively small numbers of NHS staff) were the clinically extremely vulnerable.
So, in those early months we are simply looking at the all-cause death rates of the clinically extremely vulnerable vs those who are not. It should not take a genius to understand why the the former is significantly higher than the latter.
And this is promising. If we focus down more and more, we should be able to discover many atypical groups, where the all-cause death rates go all over the place. And it turns out you can - and there are many, many variations on the theme. It’s especially effective if you cut by dose number, by time AND by age.
For example, let’s take - say 70-80 year olds, and choose a single month - May 2023. If we break down the rates by dose, it turns out that while the unvaccinated have quite a high death rate, those with a single dose in May 2023 have an even higher one.
You can display this - and many similar charts to show the danger of the vaccine (if you’re feeling particularly mulish, you can even exclude the multiple dose lines to emphasise the effect you want).
Of course, you have to distract your audience from something rather important. That “one dose” group is tiny - less that 1% of the total. Even the small “unvaccinated” group is much larger, and the two, three and four dose groups are fully 90x larger than the tiny one-dose group.5
And it’s also a very weird group. Second dose appointments are made automatically in the system once you book your first, so we here are looking at a set representing <1% of their age-groups, and one who we are selecting for their habit of missing NHS appointments - so one might suspect they may have other issues that might need to be taken into account. But if we focus all the attention on them, and ignore the other 99% of the people in the sample, who show progressively more protection leading to progressively more vaccination protection, then - again - we have a powerful set of tools to mislead. And, don’t get confused on your rhetoric: It’s: “Let’s look in detail!” when you want to focus on one particular subset. And it’s “Count all the deaths!” when you want to substitute in new denominators. Don’t get them mixed up.
Now, these approaches may seem pretty basic (and somewhat desperate, when viewed dispassionately), but it’s striking how far variations on these four themes: lying about methodology, railing against age-standardisation, switching denominators, and focusing on tiny unrepresentative groups, can get you. Video-length in many cases. Article length too.
Of course merely recognising the component techniques doesn’t get you to mastery. In the same way that recognising that a conjurer is just using palming, switching, vanishes and reveals, does not get you to the effects they can produce, especially with a bit of patter (overblown rhetoric) and showmanship (yelling).
But these four techniques remain the basic building blocks of the vast majority - perhaps all - of the anti-vaccine screeds that mention the ONS and similar datasets.
The vaccinated group have a low, more or less consistent death rate, only suffering as the first flu wave arrives in December 2022. The unvaccinated start a sky-high death rate (partly due to COVID, partly due to the fact that the unvaccinated tend to be poorer, less educated, and have a lower socio-economic status than the vaccinated), and both these effects diminish over time as the unvaccinated gain natural immunity, the Omicron variant comes through, and extended outreach efforts get to harder-to-reach groups.
Also, there’s a rather brutal selection effect, as the higher mortality rate in the unvaccinated “selects” for poor health.
By the end of the time series, the unvaccinated are only dying slightly more (like 7% more) than the vaccinated.
And I do mean the opposite. That is, to acknowledge that the data is high quality, but attempt to reverse the conclusion. Another approach is to try to discredit the data altogether, e.g., by noting that non-age confounders still remain in the data. Which they do, which the ONS points out repeatedly, and which can be seen by looking at the non-COVID death rates, which also differ between the groups.
Sticking to just the most important factors: those who choose to be vaccinated are of a higher-socio-economic status, more likely to be employed, and considerable are richer than those who choose not to be. And these things correlate strongly with good health, so the vaccinated would die less even if the vaccine did nothing at all. I try to quantify this effect here.
Beware, the effect will diminish as the vaccination programme proceeds down the ages, but you can then repeat the trick with further booster doses, which tend to be reserved for older ages.
One approach might be to protest that you have good reason to believe that the remaining 8.4% of the population may have very different rates to the rest of the population. And they almost certainly will do for almost any measure you can think of. By definition, they are unlinkable to NHS records, which is often a signal of being an overseas national, homeless, or “off-UK-grid” in some other way - they are extremely untypical. But piling them on top of alternative denominators doesn’t do anything to “include” them, especially when the uncertainty on the denominator has just swamped the entire signal you claim you are looking for.
All the sizes of every group in every month are provided in the ONS dataset. They are given in person-years, so if you want a raw count of the average number of people, in some given month just divide by 12 (or, more precisely, divide by 365 and then multiply by 28, 30 or 31, depending on which month you are in).